La divina proporción, el número áureo, la razón dorada, son algunos de los nombres que recibe una de las tres cifras irracionales más famosas de la historia, junto con el número pi y el número e de los logaritmos neperianos. Te invitamos a conocerla en 7 interesantes notas.
7 extraordinarias cosas que tienes que saber sobre el número de oro
Por:Univision
Imagen Thinkstock
Imagen Thinkstock
7. La perfección de la irracionalidad
Primero recordemos que un número irracional es todo número real que no es racional. Los números racionales son enteros o tienen una expresión decimal, bien finita o bien infinita y periódica, siendo esta última la que se repite de manera indefinida (ejemplos: 0,3333333… y 0,142857142857…). En cambio, los números irracionales tienen una expresión decimal infinita y aperiódica y no pueden proceder del cociente entre dos números enteros.
- También te recomendamos leer: «Tau: El sucesor de pi»
Imagen Wikimedia Commons
6. La razón dorada
Nuestro mítico número, asociado a la naturaleza, la belleza y el arte, incluso hasta el abuso, es el 1,6180339887498... Los puntos suspensivos significan que el número va sumando decimales hasta el infinito, sin que haya un patrón «racional» en el encadenamiento de dígitos.
La gloriosa proporcionalidad fue definida por un matemático de la antigüedad, no se sabe quién, sin imaginar las consecuencias de su ocurrencia. Este científico desconocido dibujó una recta, quizá con un dedo en la tierra, y la dividió en dos segmentos, uno (a), más largo que otro (b) y luego enunció que el cociente entre la longitud total de la recta (a + b) y la del segmento más grande (a), debía ser igual al cociente entre la del segmento grande (a) y la del pequeño (b).
La igualdad descrita se resuelve mediante una ecuación de segundo grado en la que a/b, o (a + b)/a, es igual a 1,6180339887498..., la divina proporción, la razón dorada.
- Te recomendamos leer también: «Fractales: el arte de la matemática»
Imagen Thinkstock
5. Famosas referencias a la mítica cifra
Convertido por la historia en algo parecido a un mito, al número se le atribuyen referencias, reales o algo forzadas, por parte de personajes famosos. En algunas observaciones de Platón, hay quienes ven al número áureo, si no de bulto, al menos semiescondido. Tres siglos a. e. c. Euclides, el matemático considerado el padre de la geometría, estudió el número en su célebre tratado Elementos.
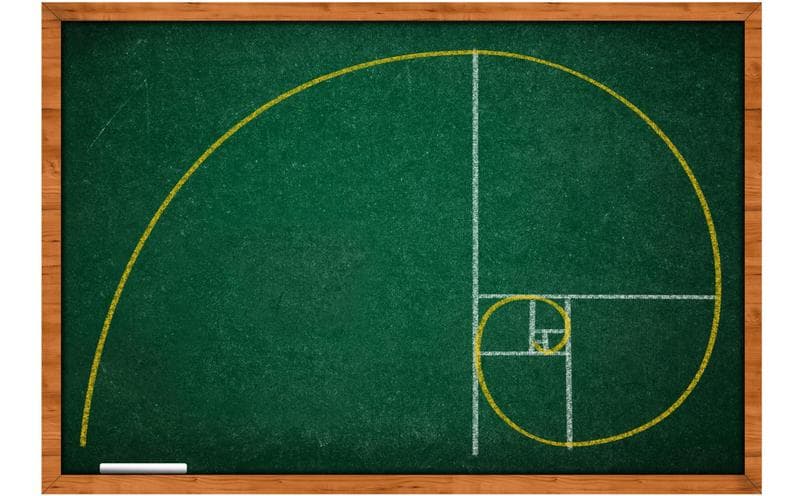
El fundador del Renacimiento alemán, Alberto Durero, enseñó en su obra Instrucción sobre la medida con regla y compás de figuras planas y sólidas, cómo trazar la espiral dorada valiéndose solo de esos antiquísimos instrumentos. Esta bonita figura, conocida también como « Espiral Durero» surge de un gran rectángulo dorado y otros internos más pequeños.
El rectángulo dorado (posiblemente tengas alguno en la cartera: una de tus tarjetas de crédito) es aquel que proporcionalmente tiene por lado largo 1,61803 y por lado corto la unidad. El matemático y astrónomo alemán, Johannes Kepler, autor de las leyes sobre el movimiento de los planetas, también se sintió atraído por el número y le dedicó unas líneas, aunque más poéticas que científicas.
- Quizá también te interese leer: «3,14: celebremos el día de Pi con 5 curiosidades»
Imagen Thinkstock
4. El primero en llamarlo número dorado
El primero en utilizar el término « razón áurea» fue Martin Ohm, el matemático alemán del siglo XIX que desarrolló la teoría exponencial con números complejos. No obstante el glamour de haber bautizado al afamado número, el Ohm más famoso no es Martin sino su hermano Georg, quien fue el autor de la conocida Ley de Ohm, que relaciona voltaje, intensidad y resistencia en las corrientes eléctricas.
- También te recomendamos leer: «¿Conoces la curiosa e interesante importancia del número 2 147 483 647?»
Imagen Thinkstock
3. La razón dorada en la naturaleza y en el arte
La divina proporción lineal, o su equivalente en las figuras geométricas, ha sido identificada en las relaciones de distancias entre órganos del cuerpo humano, en nervaduras y hojas, ramas y troncos, pétalos de las flores, la espiral de los caracoles, los minerales cristalizados y cualquier cantidad de formaciones naturales.
Al parecer, la naturaleza no sale de casa sin el número dorado. También en el arte, la razón áurea es vista, real o imaginariamente, en todas partes. En el Partenón de Atenas, en el David de Miguel Ángel, en las grandes obras de Leonardo.
- Quizá también te interese leer: «6 mensajes escondidos en grandes obras de arte que te dejarán boquiabierto»
Imagen Thinkstock
2. Más perfección, imposible
Si elevas el número dorado al cuadrado, obtienes 2,618033988... y si calculas su inverso el resultado es 0,618033988... ¡el mismo componente decimal en ambas cifras, el colmo de la perfección!
- Ver más: «Número áureo: La divina proporción»
Imagen Thinkstock
1. Dorado hasta en la sopa
No nos referimos a un caldo del conocido pez de río. Desde hace tiempo se cree que las cosas hechas siguiendo la divina proporción son más agradables a la vista. Los carpinteros que están en el ajo, fabrican sus mesas rectangulares de acuerdo con la atractiva proporcionalidad. El marketing de productos y empaques la utiliza hasta la saciedad. Incluso, hay gente que cree que algunas personas siguen atadas al dañino hábito de fumar porque están subyugadas por la perfección geométrica de la cajetilla de cigarrillos. Parece exagerado, pero ….
¿Conocías la razón dorada? ¿Qué te ha parecido?
- Te recomendamos leer también nuestro artículo: «¿Qué es la sucesión de Fibonacci?»
Relacionados: